1. Eurocall
Page Content
Wolfram Oracle
Wolfram app-id (use your own, https://products.wolframalpha.com/simple-api/documentation):
Cors proxy prefix (to query wolfram services):
BTC price is: (lock)
source: Wolfram Alpha
Marlowe Contract
Let's generate marlowe European Call contract first. Alice and Bob are betting on BTC price. The risk is amortized for small price changes between Alice's premium at risk and Bob's margin at risk, leveraged by notional. The deal is P2P, thus fully collatrerized, no "pooled margin account" risks involved.
Cardano version: https://github.com/dk14/marlowe-wolfram-starter-kit/blob/main/22-eurocall.ipynb
Contract terms:
- Contract strike is usd
- Alice pays premium of usd
- Notional/Leverage is btc
- Bob's margin is usd
- Oracle range is to
Note: this is webarchived slightly edited SNAPSHOT of open source Marlowe Playground, NOT ACTUAL PLAYGROUND BY IOHK (see https://replayweb.page/docs/wacz-format, actual Playground might differ: https://play.marlowe.iohk.io/, https://github.com/input-output-hk/marlowe-playground). Do NOT trust this for any other purposes than educational. Generator auto-fills the contract for you (since original playground doesn't support that), so you could simulate the contract. USE actual https://play.marlowe.iohk.io/ for contract development.
Sampling
Let's sample Marlowe contract and plot the payoff curve. Note: contract has to be generated first
Prepare Oracle R and s values for Bitcoin DLC
Warning: Don't use any of it with actual Bitcoin mainnet - educational purposes only
Oracle quesion:
Oracle secret (hex):
Oracle's public key:
\(V = secret \circ G\)
Oracle's secret k-value:
\( k= hash(secret_{oracle} G || hash(aux) || question) \mod n \)
(Security note: k-value is derived from hash-encrypted question)
Oracle's public commited R-value:
\( R=kG \)
(this value is returned by the oracle API when someone is asking for a question that is not answered yet)
Oracle's future answer:
Tweaked public key (adaptor point), contract parties derive it from R, possible answer and oracle's public key
\( Pub_{Alice, question} = Pub_{Alice} + s_{answer}G\),
where \(s_{answer}G = R − hash(answer || R)V\)
When the answer is ready...
Oracle publishes s-value (signature):
(Note: signature is derived from pre-commited k-value, thus R-value part would be commited R-value as well)
This value is gonna be used as a secret (private key corresponding to adaptor public key) to co-sign CET transactions in case of dispute.
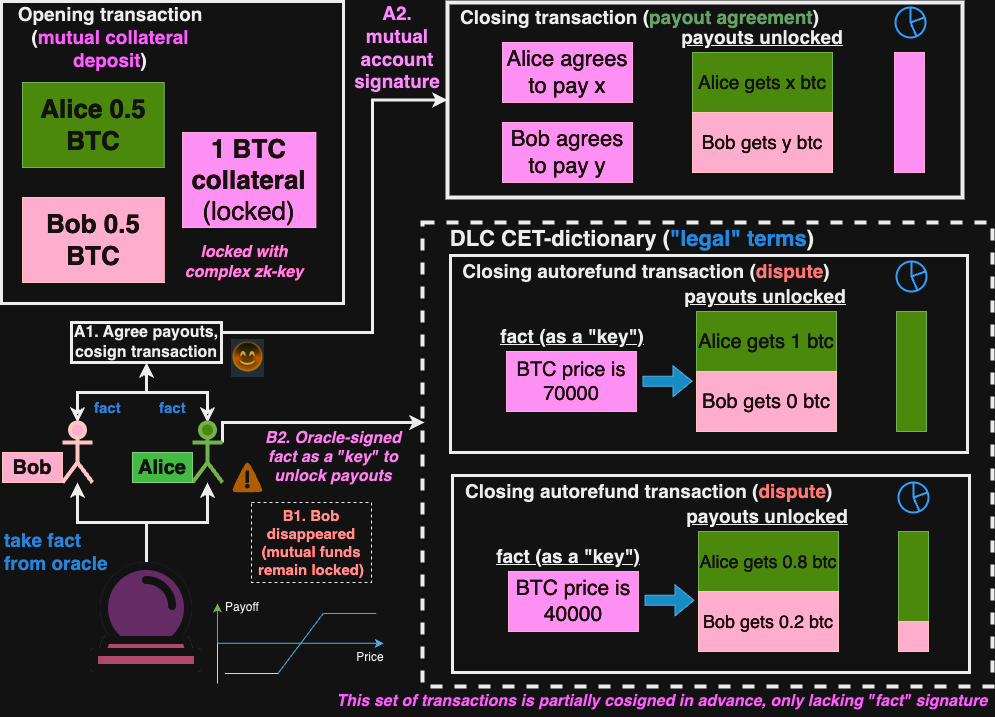
Prepare Transactions for Bitcoin DLC
Original DLC paper: https://adiabat.github.io/dlc.pdf
DLC and Oracles: https://docs.google.com/document/d/1TVYvpZwwGLrSYHtnpoEoSE1csMSZfZ-A7xF9w0viMIs/edit?usp=sharing
Decode TX hexes (choose Testnet): https://live.blockcypher.com/btc/decodetx/
Alice:
- secret (hex):
- utxo value:
- txid (hex):
- vout:
Bob:
- secret (hex):
- utxo value:
- txid (hex):
- vout:
\(OpeningTx: txin_{AliceCollateral}(Pub_{Alice}) + txin_{BobCollateral}(Pub_{Bob}) = txout_{JointCollateral}(Pub_{Alice} + Pub_{Bob})\)
Opening TxId:
Opening Hex:
\(ClosingTx: txin_{JointCollateral}(Pub_{Alice} + Pub_{Bob}) = txout_{AlicePayoff}(Pub_{Alice}) + txout_{BobPayoff}(Pub_{Bob})\)
Closing TxId:
Closing Hex:
\(DisputeTx: txin_{JointCollateral}(Pub_{Alice} + Pub_{Bob}) = txout_{AlicePayoff}(Pub_{Alice} + s_{answer}G) + txout_{BobPayoff}(Pub_{Bob})\)
\(s_{answer}G\) is known in advance, while \(s_{answer}\) will be published by Oracle
Dispute CET TxId:
Dispute CET Hex:
\(RedemptionTx: txin_{AlicePayoff}(Pub_{Alice} + s_{answer}G) = txout_{AlicePayoff}(Pub_{Alice}) \)
\(signature = (s_{Alice} + s_{answer}) || (R_{Alice} + R_{question})\)
Dispute Redemption TxId:
Dispute Redemption Hex: